مساحة شبه المنحرف وطريقة استنتاجها الصحيحة
شبه المنحرف هو عبارة عن شكل هندسي رباعي الأضلاع، يكون فيه اثنان من الأضلاع المتقابلة متوازيان، ويمكن تعريفه على أنه رباعي أضلاع له فقط ضلعين متقابلين متوازيين، وبالتالى يتم استثناء متوازي الأضلاع من التعريف، الذي غالباً ما يعتبر حالة خاصة من شبه المنحرف، ونعرض في هذا المقال مساحة شبه المنحرف .
مساحة شبه المنحرف
هناك عدة طرق لحساب المساحة لشبه المنحرف ، نعرض منها، ما يلي، حيث تُحسب مساحة شبه المنحرف من المعادلات الرياضية الآتية:
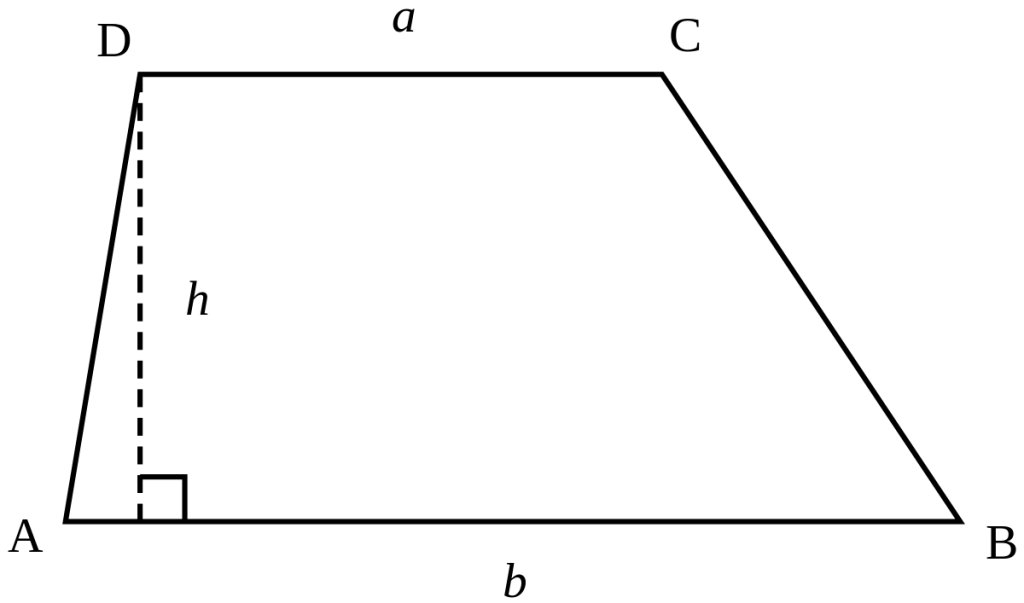
- مساحة شبه المنحرف = ( طول القاعدة الكبرى + طول القاعدة الصغرى) % 2 ) × الارتفاع.
- أى أن مساحة شبه المنحرف تساوى مجموعة القاعدتين مقسومة على ٢ ومضروبة في الارتفاع، حيث يُعد الارتفاع في شبه المنحرف هو ضلع عمودى على القاعدة الكبرى أي بزاوية ٩٠ درجة مئوية ( زاوية قائمة )، أما في أنواع شبه المنحرف الأخرى يكون الارتفاع هو المسافة العمودية بين القاعدتين المتوازيتين.
- يمكن حساب المساحة عن طريق تقسيم شبه المنحرف إلى أشكال هندسية، مثل مستطيل ومثلث، أو مربع ومثلث، أو متوازي أضلاع ومثلث.
- ويكون الهدف من هذا التقسيم، هو إيجاد شكل هندسي يسهل حساب مساحته، عن طريق حساب مساحة كل شكل هندسي على حدى، ومن ثم جمع مساحتى الشكلين الهندسيين معًا، لحساب مساحة شبه المنحرف، فمثلاً يمكن تقسيم شبه المنحرف إلى ثلاث أشكال، مستطيل ومثلثين، لتكون بذلك:
مساحة شبه المنحرف = مساحة المثلث الأول + مساحة المثلث الثاني + مساحة المستطيل.
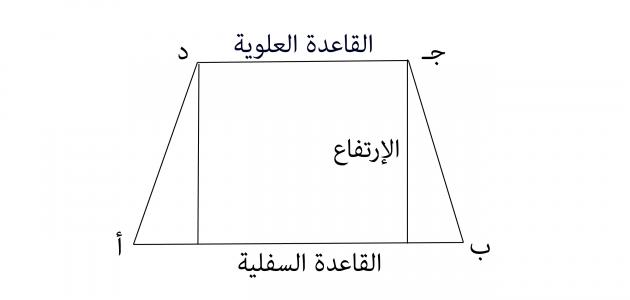
أنواع شبه المنحرف
تعدد أنواع شبه المنحرف، وتختلف، مما يعني اختلاف المعادلات الحسابية لإيجاد كلاً من المساحة والمحيط لكل نوع من أنواع شبه المنحرف كما سبق الذكر، لذلك نعرض أنواع شبه المنحرف، والتي تتمثل في:
- شبه منحرف عام، وهو عبارة عن مضلع رباعي، له ضلعان متوازيان، وقطران غير متساويان يتقابلان في نقطة ما، وبالتالي فإن الارتفاع في هذا النوع من أنواع شبه المنحرف هو المسافة العمودية بين الضلعين المتوازيين، وبذلك يحتوى هذا النوع من أنواع شبه المنحرف على أربع زوايا غير متساوية مجموع قياسها ٣٦٠ درجة مئوية، بالإضافة إلى أن مجموع الزاويتين المحصورتان بين الضلعين المتوازيين هو ١٨٠ درجة مئوية.
- شبه منحرف متساوي الساقين، ويكون فيه ضلعان متقابلان متوازيان، والضلعين الآخرين متقابلان ومتساويان في الطول وغير متوازيين، أما فيما يخص طول قطريه فهو متساوي.
- شبه منحرف مختلف الأضلاع، وهو عبارة عن أربع أضلاع، اثنان منهم متوازيان غير متساويان، وهما يمثلان قاعدتي شبه المنحرف، والضلعين الآخرين غير متوازيين وغير متساويين، وله قطران غير متساويان، يتقاطعان في نقطة ما.
- شبه منحرف قائم الزاوية، وهو عبارة عن زاويتين قائمتين، والارتفاع يمثل الضلع العمودي على القاعدة الكبرى، في هذا النوع من أنواع شبه المنحرف، ويُعد الارتفاع أو الضلع العمودي على القاعدة هو أحد أهم أضلاع شبه المنحرف.
مساحة شبه المنحرف غير منتظم
شبه المنحرف غير المنتظم هو عبارة عن شبه منحرف مكون من أربع أضلاع غير متساوية في الطول، وتُحسب المساحة لشبه المنحرف غير المنتظم معلوم الأبعاد من المعادلة الحسابية الآتية:
- مساحة شبه المنحرف غير المنتظم = ½ × مجموع القاعدتين × الارتفاع.
ومثال على ذلك:
شبه منحرف غير منتظم، أطوال قاعدتيه 4 و12 سم على التوالي، ويبلغ ارتفاعه 8 سم، احسب مساحته.
الحل:
مساحة شبه المنحرف غير المنتظم= ½ × مجموع القاعدتين × الارتفاع.
فإن مساحة شبه المنحرف غير المنتظم= ½ × (12+4) × 8= 64 سم2.
- أما فيما يخص مساحة شبه المنحرف غير المنتظم مجهول الارتفاع، فإن الأطوال والزوايا المعطاة المذكورة في المثال، تستخدم لإيجاد الارتفاع، عن طريق تطبيق قواعد النسب المثلثية، ويمكن توضيح ذلك بالمثال الآتي:
شبه منحرف غير منتظم، طول القاعدة الأولى له = 16 سم، وطول القاعدة الثانية= 25 سم، وطول أحد ساقي شبه المنحرف= 12 سم، أما الزاوية بين الساق والقاعدة الثانية =30 درجة، احسب مساحته.
الحل:
باستخدام قانون فيثاغورس أو قواعد الجيب وجيب التمام، يمكن إيجاد الارتفاع، حيث يستخدم قانون جيب الزاوية في الحصول على الارتفاع باستخدام جيب الزاوية 30، ومن خلال القانون؛ فإن:
جا (الزاوية)= الارتفاع / الوتر.
جا 30 = الارتفاع / 12 سم.
وبالتالي فإن الارتفاع= 6 سم.
وبعد معرفة قيمة الارتفاع، يمكن حساب المساحة باستخدام الصيغة الخاصة بمساحة شبه المنحرف؛ مساحة شبه المنحرف= ½ × مجموع القاعدتين × الارتفاع.
مساحة شبه المنحرف غير المنتظم= ½ × (16+25) × 6= 123 سم2.
قد يهمك أيضا: كيفية فصل الصوت عن الموسيقى للكمبيوتر والأندرويد
استنتاج مساحة شبه المنحرف
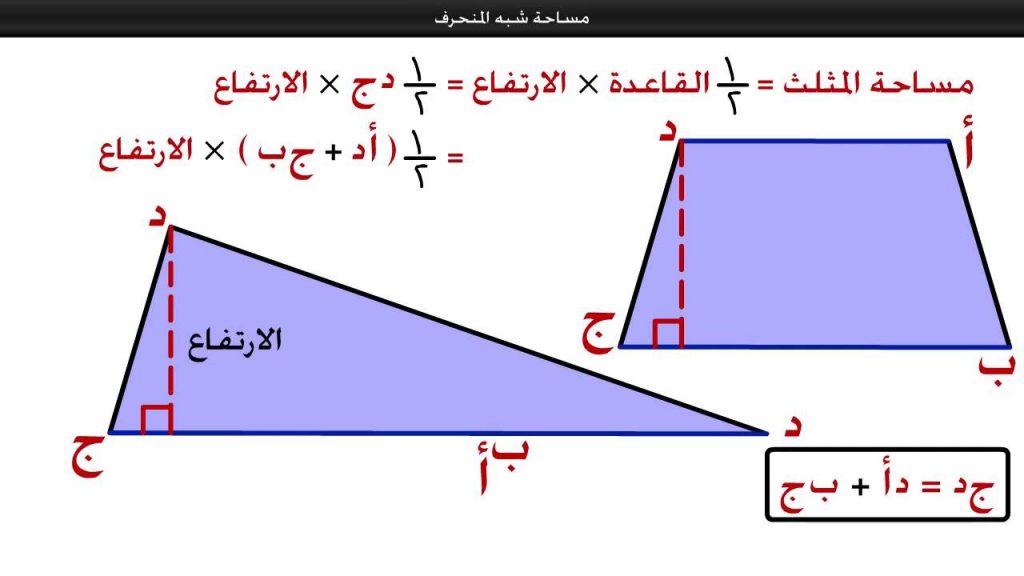
كما هو المعروف في الرياضيات أو حتى الفيزياء، فإن أى صيغة معادلة حسابية، لابد أن تكون قد نتجت عن طريق الاستنتاج من عدة صيغ ومعادلات حسابية أخرى، لذلك نعرض في هذا المقال استنتاج مساحة شبه المنحرف ، والتي تتمثل في الآتي:
- يمكن تكوين متوازي أضلاع من شبه منحرف، بحيث يتساوى في ارتفاعه مع ارتفاع شبه المنحرف، وطول قاعدته يساوي مجموع طولا قاعدتي شبه المنحرف.
- حيث يمكن أن يتكون متوازي الأضلاع من شبهي منحرف متطابقين نتيجة دوران شبه المنحرف الأول حول أحد طرفي القاعدة.
- وبما أن مساحة متوازي الأضلاع يمكن حسابها من القانون التالي:
- مساحة متوازي الأضلاع = حاصل ضرب طول القاعدة ×الارتفاع.
- فإن مساحة شبه المنحرف = ½ ( مجموع طولا قاعدتيه )× الارتفاع.
قد يهمك أيضا: تعريب اوفيس 2016
محيط شبه المنحرف
محيط شبه المنحرف هو المسافة المحيطة بشبه المنحرف، أو بمعنى آخر هو مجموع أطوال أضلاع شبه المنحرف، ويمكن حساب محيط شبه المنحرف عن طريق تطبيق عدة صيغ معادلات حسابية وقوانين، والتى تتمثل فى الآتى:
- محيط شبه المنحرف = مجموع أطوال أضلاعه.
- محيط شبه المنحرف = القاعدة العلوية + القاعدة السفلية + الارتفاع×((1/جا زاوية القاعدة اليمنى) + (1/جا زاوية القاعدة اليسرى)).
- أى محيط شبه المنحرف = أ+ب+ع×((1/جاس) + (1/جاص)).
- حيث: أ، وب: هما قياس الضلعين المتقابلين، والمتوازيين في شبه المنحرف.
- ع: ارتفاع شبه المنحرف.
- س، ص: هما الزاويتان المحصورتان بين القاعدة السفلية، والضلعين غير المتوازيين.
- محيط شبه المنحرف متساوي الساقين: يمكن حساب محيط شبه المنحرف متساوي الساقين باستخدام القانون الخاص الآتي: محيط شبه المنحرف= أ+ب+ 2 ج.
- حيث: أ، وب: هما طول الضلعين المتوازيين في شبه المنحرف.
- جـ: هو طول أحد الضلعين غير المتوازيين في شبه المنحرف، ومتساويان في الطول.
- محيط شبه المنحرف القائم: وهو شبه منحرف فيه زاويتان قائمتان، ويمكن إيجاد محيط شبه المنحرف القائم من خلال العلاقة الآتية:
- المحيط = أ+ع1+ع2+ الجذر التربيعي للقيمة (أ²+(ع2 – ع1)².
- حيث: أ: هو طول أحد أضلاع شبه المنحرف، وهو الضلع القائم على الضلعين الآخرين.
- ع1: هو طول أحد الضلعين المتوازيين لشبه المنحرف (الضلع الأول).
- ع2: طول أحد الضلعين المتوازيين لشبه المنحرف (الضلع الثاني).
وبذلك نكون قد عرضنا في هذا المقال، مجموعة لا بأس بها من قوانين شبه المنحرف، التي تتمثل في مساحة شبه المنحرف لجميع أنواع شبه المنحرف، ومساحة شبه المنحرف غير المنتظم، مع ذكر أنواع شبه المنحرف، وقوانين محيط شبه المنحرف، واستنتاج قانون مساحة شبه المنحرف.
قد يهمك أيضا: شفرات جاتا سان اندرس






